Queue
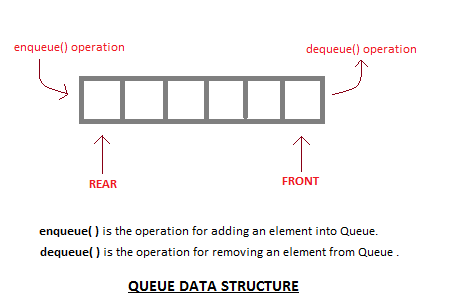
A queue is non-premitive linear data structure . It is based on first-in-first-out (FIFO) mechanism.In queue deletion can take place at one end of the list , the front of the list. And insertion can take place at the other end of the list , rear of the list.
Queues are often usde in programming networks , operating systems , and other situations in which many different processes must share resources such as CPU time.


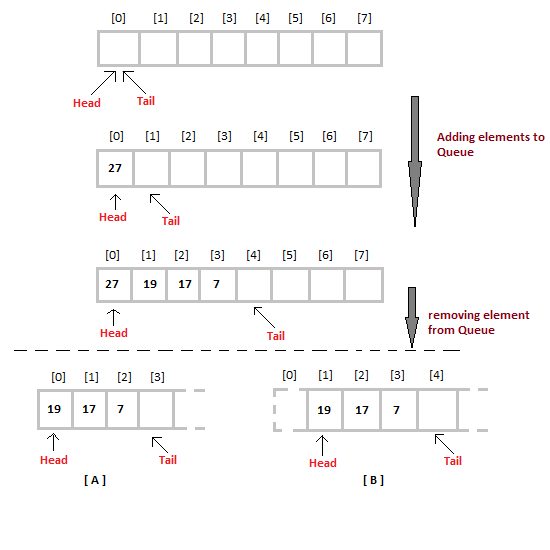
Many operations can be possible on a queue as:-
Step 1: [ Check for ovetflow condition]
If rear>= size of array then
Output:-"queue is overflow" and exit.
Step 2: [Increment rear pointer]
rear=rear+1
Step 3: [Insert an element]
Q[rear]=value
Step 4: [Set the front pointer]
If
front =0 then,
front =1
step 5: return
* Algorithm for deletion (pop operation):-
Step 1: [check for underflow condition]
If front =0 then,
output:- "queue is underflow" and exit.
Step 2: [remove the element]
value=Q[rear]
Step 3: [check for empty queue]
If front =rear then,
front=0
rear=0
Else
front =front+1
Step 4: return
* There are mainly three types of queues are possible:--
i> Circular queue.
ii> Double ended queue.
iii> Priority queue.
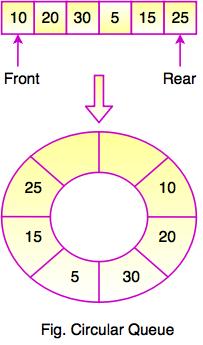
i> Circular Queue:-
In a normal queue , we can insert elements untill queue becomes full. But once queue becomes full , we cannot insert the next element . The circular is dsigned to overcome the limitations of simple queue.
Circular Queue is a linear data structure in which the operations are performad based on FIFO principle and last position id connected back to the first position to make a circle.
Suppose we have an array Q that contains n elements in which Q[1] comes after Q[n] pocket in the array. When this technique is used then the queue is called circular queue. Thus we can say that a queue is called circular when the last room comes just before the first room.

* Algorithm to insert element in circular queue:-
Step 1: [Check for overflow condition ]
If
front=1 and rear=n then,
output:- "queue is overflow" and exit.
Step 2: [Insert element in the queue]
Else if
front=0 then,
front=1
rear=1
Q[rear]=value
Step 3: [check if the rear at the end of the queue]
Else if
rear=n then,
rear=1
Q[rear]=value
Step 4: [Insert the element]
Else
rear=rear+1
Q[rear]=value
Step 5: return
* Algorithm to delete an elment from a circular queue:-
Step 1: [Check for underflow condition]
If
front =0 then,
output:- "Queue is underflow" and return.
Step 2: [remove the element]
value=Q[front]
Step 3: [Check whether the queue is empty or not]
If
front =rear then
front =0
rear=0
Step 4: [Check the front pointer position]
Else if
front =n then,
front =1
Else
front =front +1
Step 5: [Return the removed element]
return(value)
Rest two types of queue are remaining .
Will be publish on next post.😊
A queue is non-premitive linear data structure . It is based on first-in-first-out (FIFO) mechanism.In queue deletion can take place at one end of the list , the front of the list. And insertion can take place at the other end of the list , rear of the list.
Queues are often usde in programming networks , operating systems , and other situations in which many different processes must share resources such as CPU time.
* Working Process on Queue :-
- By incrementing rear pointer we can insert an element in queue.
- By incrementing front pointer we can removew element from queue.
- If queue is empty then front and rear pointer must be incremented by 1 first time.
- When rear=size- 1 then queue is full.
- When front=rear then reset front=-1 and rear=-1.
- When front=rear=-1 then the queue is empty.
Queue is different from stack in many cases. Both are non-premitive linear data structure but the mechanisms on insertion and deletion are fully different. Where queue is based on FIFO mechanism, stack is based on LIFO mechanism.
Best example of queue is the row at the ticket counter for any shows. The person who came first take ticket first , thus follows FIFO rule.
Many operations can be possible on a queue as:-
Step 1: [ Check for ovetflow condition]
If rear>= size of array then
Output:-"queue is overflow" and exit.
Step 2: [Increment rear pointer]
rear=rear+1
Step 3: [Insert an element]
Q[rear]=value
Step 4: [Set the front pointer]
If
front =0 then,
front =1
step 5: return
* Algorithm for deletion (pop operation):-
Step 1: [check for underflow condition]
If front =0 then,
output:- "queue is underflow" and exit.
Step 2: [remove the element]
value=Q[rear]
Step 3: [check for empty queue]
If front =rear then,
front=0
rear=0
Else
front =front+1
Step 4: return

* There are mainly three types of queues are possible:--
i> Circular queue.
ii> Double ended queue.
iii> Priority queue.
i> Circular Queue:-
In a normal queue , we can insert elements untill queue becomes full. But once queue becomes full , we cannot insert the next element . The circular is dsigned to overcome the limitations of simple queue.
Circular Queue is a linear data structure in which the operations are performad based on FIFO principle and last position id connected back to the first position to make a circle.
Suppose we have an array Q that contains n elements in which Q[1] comes after Q[n] pocket in the array. When this technique is used then the queue is called circular queue. Thus we can say that a queue is called circular when the last room comes just before the first room.

* Algorithm to insert element in circular queue:-
Step 1: [Check for overflow condition ]
If
front=1 and rear=n then,
output:- "queue is overflow" and exit.
Step 2: [Insert element in the queue]
Else if
front=0 then,
front=1
rear=1
Q[rear]=value
Step 3: [check if the rear at the end of the queue]
Else if
rear=n then,
rear=1
Q[rear]=value
Step 4: [Insert the element]
Else
rear=rear+1
Q[rear]=value
Step 5: return
* Algorithm to delete an elment from a circular queue:-
Step 1: [Check for underflow condition]
If
front =0 then,
output:- "Queue is underflow" and return.
Step 2: [remove the element]
value=Q[front]
Step 3: [Check whether the queue is empty or not]
If
front =rear then
front =0
rear=0
Step 4: [Check the front pointer position]
Else if
front =n then,
front =1
Else
front =front +1
Step 5: [Return the removed element]
return(value)

Rest two types of queue are remaining .
Will be publish on next post.😊

Comments
Post a Comment
Please comment.